【高数】函数与极限
本文共 674 字,大约阅读时间需要 2 分钟。
什么是函数?
设x和y是两个变量,D是一个给定的非空数集,如果按照某个对应法则f,对于每个数x∈D,变量y都有唯一确定的值和它相对应,则称这个对应法则f为定义在D上的函数。数集D称为这个函数的定义域,x称为自变量,y称为因变量。一些具体的函数:幂函数、指数函数、对数函数、三角函数、反三角函数、常数函数、绝对值函数、符号函数sgn、取整函数、分段函数。
函数的四种性质:有界性、单调性、奇偶性、周期性。
什么是函数的极限?
自变量趋于有限值时的函数的极限: 设函数f(x)在点x0的某个去心邻域内有定义,如果存在常数A,使得对于任意给定的正数ε(不论它多么小),总存在正数δ,只要点x适合不等式0<|x-x0|<δ,对应的函数值f(x)都满足不等式|f(x)-A|<ε,那么常数A就叫做f(x)当x→x0时的极限。如果这样的常数不存在,那么称x→x0时f(x)没有极限。
自变量趋于无穷大时函数的极限:
设函数f(x)在|x|>M时有定义(M为一正数)。如果存在常数A,使得对于任意给定的正数ε(不论它多小),总存在X,只要自变量x适合不等式|x|>X,对应的函数值f(x)就都满足不等式|f(x)-A|<ε,那么常数A就叫做函数f(x)当x→∞时的极限。如果这样的常数不存在,那么称x→∞时f(x)没有极限。极限的局部保号性:
如果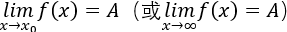 ,而且A≠0,那么存在着某个正数δ(或正数X),当0<|x-x0|<δ(或|x|>X)时,f(x)恒不为零且与A有相同的符号。这条性质说明:在自变量的一个局部变化范围内,函数值f(x)与极限值A保持相同的符号。
,而且A≠0,那么存在着某个正数δ(或正数X),当0<|x-x0|<δ(或|x|>X)时,f(x)恒不为零且与A有相同的符号。这条性质说明:在自变量的一个局部变化范围内,函数值f(x)与极限值A保持相同的符号。 转载地址:http://avvh.baihongyu.com/
你可能感兴趣的文章